

Strength of materials, also know as mechanics of materials, is focused on analyzing stresses and deflections in materials under load. Knowledge of stresses and deflections allows for the safe design of structures that are capable of supporting their intended loads.
Related Pages:When a force is applied to a structural member, that member will develop both stress and strain as a result of the force. Stress is the force carried by the member per unit area, and typical units are lbf/in 2 (psi) for US Customary units and N/m 2 (Pa) for SI units:
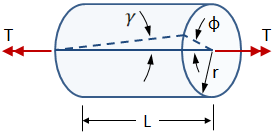
where ϕ is the angle of twist, r is the radius of the bar and L is the length.
The shear strains are proportional through the interior of the bar, and are related to the max shear strain at the surface by:
ρ is the radial distance from the bar's axis.
Stress is proportional to strain in the elastic region of the material's stress-strain curve (below the proportionality limit, where the curve is linear).
Normal stress and strain are related by:
where E is the elastic modulus of the material, σ is the normal stress, and ϵ is the normal strain.
Shear stress and strain are related by:
where G is the shear modulus of the material, τ is the shear stress, and γ is the shear strain. The elastic modulus and the shear modulus are related by:
ν is Poisson's ratio.
Hooke's law is analogous to the spring force equation, F = k δ . Essentially, everything can be treated as a spring. Hooke's Law can be rearranged to give the deformation (elongation) in the material:

When force is applied to a structural member, that member deforms and stores potential energy, just like a spring. The strain energy (i.e. the amount of potential energy stored due to the deformation) is equal to the work expended in deforming the member. The total strain energy corresponds to the area under the load deflection curve, and has units of in-lbf in US Customary units and N-m in SI units. The elastic strain energy can be recovered, so if the deformation remains within the elastic limit, then all of the strain energy can be recovered.
Strain energy is calculated as:
We have a number of structural calculators to choose from. Here are just a few:
Stiffness, commonly referred to as the spring constant, is the force required to deform a structural member by a unit length. All structures can be treated as collections of springs, and the forces and deformations in the structure are related by the spring equation:
where k is the stiffness, F is the applied force, and δmax is the maximum deflection deflection in the member.
If the deflection is known, then the stiffness of the member can be found by solving k = F/δmax . However, the maximum deflection is typically not known, and so the stiffness must be calculated by other means. Beam deflection tables can be used for common cases. The two most useful stiffness equations to know are those for a beam with an axially applied load, and for a cantilever beam with an end load. Note that stiffness is a function of the material's elastic modulus, E , the geometry of the part, and the loading configuration.
 |
| Extreme Shear Stress Angles: |
The angles above can be substituted back into the transformation equations to find the values of the principal stresses and the extreme shear stresses:
The state of stress on the x and y faces of the stress element is represented by the black line in Mohr's circle connecting the points ( σx , −τ ) and ( σy , τ ). This line in Mohr's circle corresponds to the unrotated element in the figure below. If this line is rotated by some angle, then the values of the points at the end of the rotated line will give the values of stress on the x and y faces of the rotated element. It is important to note that the 360 degrees of Mohr's circle are equivalent to 180 degrees on the stress element. For instance, the points for x face and the y face are 180 degrees apart on Mohr's circle, but they are only 90 degrees apart on the stress element.
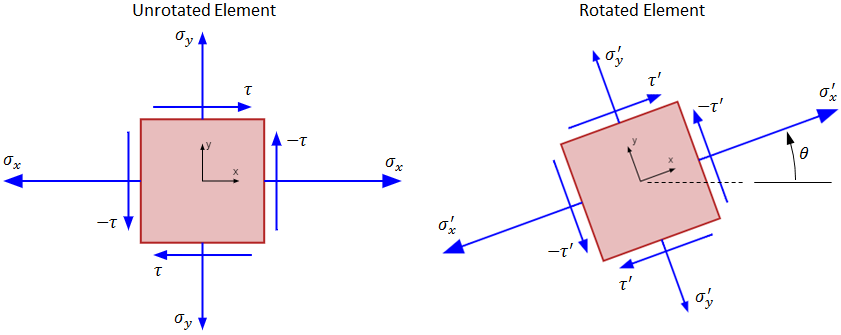
To get a more intuitive feel for how Mohr's circle relates the stresses on a stress element and how the stress state changes as a function of rotation angle, see the accompanying Mohr's circle calculator.
There are many structural components that are commonly subjected to stress analysis. The details on the analysis of these components are given in other sections:
We have a number of structural calculators to choose from. Here are just a few:

Knowledge of stresses and deflections allows for the safe design of structures that are capable of supporting their intended loads. It is always desired for the stresses in a structure to remain within the limits of the structure's strength. The yield strength of the material is commonly chosen as the strength limit to which the calculated stresses are compared.
The factor of safety, FS , is calculated as:
In the equation above, any value above zero indicates that the actual stress is below the limit stress. Although margins of safety are typically reported as decimal values, it is much more intuitive to think of margins as percentages. For example, if the limiting stress of a structure is 1.5 times higher than the actual stress, there is 50% margin ( MS = 0.5).
When reporting factors of safety and margins of safety, sometimes the required factor of safety will be "baked in" to the reported factors. For example, the engineers may require a structure to maintain a factor of safety of at least 2, so that FSreq = 2 . To bake in the required factor of safety, the reported FS and MS are calculated as:
FSreq , the reported FS and MS are actually the margins with respect to FSreq , not with respect to the stress.
PDH Classroom offers a continuing education course based on this strength of materials reference page. This course can be used to fulfill PDH credit requirements for maintaining your PE license.
Now that you've read this reference page, earn credit for it!